 |
|
 |
| |
 |
Posição de uma reta
|
 |
|
|
 |
|
 |
| |
Uma reta s = ax+by+c = 0 pode assumir três posições em relação à uma circunferência de raio r e centro C = (xc,yc): Para saber qual destas posições uma reta realmente ocupa precisamos resolver o sistema formado pela equações da reta e da circunferência: 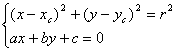
|
|
|
 |
|
 |
| |
1. A reta pode ser externa à circunferência à circunferência.
2. A reta pode ser tangente à circunferência.
3. A reta pode ser secante à circunferência.
|
 |
|
|
|
| |

|
|
| |
 |
|
| |
Externa
|
|
|
|
|
|
|
|
 |
|
 |
| |
Isolando x ou y na equação da reta e substituindo-os na equação da circunferência teremos uma equação do segundo grau, que admite três possibilidades de solução:
1. D = 0: A equação só tem uma solução, e a reta é tangente à circunferência.
2. D > 0: A equação tem duas soluções, e a reta é secante à circunferência.
3. D < 0: A equação não tem solução, e a reta é externa à circunferência.
|
 |
|
|
|
| |

|
|
| |
 |
|
| |
Tangente
|
|
|
|
|
|
|
|
 |
|
 |
| |
Qual a posição da reta 2x-y-2 = 0 em relação à circunferência x2+y2 + 2x - 4y = 0?
Isolando y = 2x - 2 na equação da reta e substituindo na da circunferência temos:
x2+(2x - 2)2 + 2x - 4(2x - 2) = 0
x2+ 4x2 - 8x + 4 + 2x - 8x + 8 = 0
5x2 - 14x + 12 = 0
D= -44
Logo, a reta é externa à circunferência, pois D<0.
|
 |
|
|
|
| |

|
|
| |
 |
|
| |
Secante
|
|
|
|
|
|
|
|
 |
|
 |