 |
|
 |
| |
 |
Introdução e conceito gerais
|
 |
|
|
 |
|
 |
| |
|
|
 |
|
 |
| |
Vamos observar este cubo.
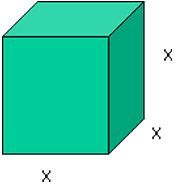
Se calcularmos sua área, teremos 6.x2. Essa representação algébrica da área do cubo é uma notação polinomial.
|
|
|
 |
|
 |
| |
|
Matematicamente, possuímos muitas formas de representações genéricas de termos e fórmulas. Assim, temos este tipo de representação também em polinômios: anxn + an-1xn-1+ an-2xn-2+...+a2x2+a1x+a0 O que cada um destes termos significa? Cada uma das representações an,an-1, an-2,...,a2,a1,a0 são chamadas de coeficientes e são números reais e n é um número positivo e diferente de zero.
|
|
|
 |
|
 |
| |
| O grau de um polinômio Sabemos o que significam equações de 1ºgrau e de 2ºgrau. |
 |
|
|
|
| |
Como poderemos encontrar o grau de um polinômio?
É simples! Observamos todos os expoentes dos coeficientes do polinômio e o maior deles representa o grau da expressão. Vamos verificar? |
|
|
|
|
|
|
|
 |
|
 |
| |
|
Outra importante informação que precisamos saber sobre polinômios é em relação ao seu valor numérico. Como encontrar o valor numérico de um polinômio P(x)?Vamos supor que x seja igual a um número qualquer chamado K, então podemos indicar matematicamente P(x) = P(k). Se P(k) for igual a zero, então K é raiz da equação. Vamos verificar como encontrar o valor numérico de um polinômio?
|
|
|
 |
|
 |
| |
| A igualdade de polinômios Vamos pensar em dois polinômios, um chamado de P(x) e outro de Q(x). Quando podemos afirmar que são iguais, ou seja, que P(x) = Q(x)? É muito importante aprendermos como identificar a Igualdade de Polinômios. |
 |
|
|
|
| |
Dois polinômios são iguais se ambos possuírem o mesmo grau e os mesmos coeficientes de seus termos.Como? Observe os dois polinômios abaixo: P(x) = ax3+bx2+cx+d e Q(x) = 4x3+2x2+x+4. Para definirmos que P(x) é igual a Q(x) temos que levar em conta se cada um dos coeficientes dos termos de ambos são iguais e se possuem o mesmo grau. Clique aqui para verificar... |
|
|
|
|
|
|
|
 |
|
 |