 |
|
|
| |
 |
Equação e inequação exponencial
|
 |
|
|
|
|
|
| |
|
Equação Exponencial Chamamos de equações exponenciais aquelas equações em que a variável x aparece nos expoentes.
|
|
|
|
|
|
| |
Por exemplo: - 3x = 27
- 2x -2 = 0
- 5x+1 = 25
Para se resolver uma equação exponencial, deve-se reduzir os dois membros da igualdade a uma mesma base, depois relembrando a propriedade 3, que diz que:
am = an 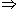 m = n (a # 1 e a > 0) Agora é só igualar os expoentes e resolver como uma equação comum.Acompanhe alguns exemplos clicando abaixo em "equação exponencial".
|
|
|
|
|
|
|
|
| |
Inequação Exponencial
Chamamos de inequações exponenciais, as desigualdades em que a variável x aparece como expoente. Veja os exemplos abaixo:
|
|
|
|
|
|
| |
- 3x-2 > 27
- 2x -2 < 0
- 5x+1 < 25
|
|
|
|
|
|
|
|
| |
Para resolvermos inequações exponenciais deve-se, primeiro, reduzir os dois membros da igualdade a uma mesma base, que vamos chamar de a. Depois devemos comparar os expoentes. É aí que devemos prestar atenção, pois pelas propriedades 4 e 5 dependendo do valor de a, teremos duas possibilidades: Para a > 1 temos:
am < an  m < n ou am > an m > n
neste caso, conserva-se o sentido da desigualdade. Para 0 < a < 1 temos:
am < an m > n ou am > an m < n
aqui, inverte-se o sentido da desigualdade. Veja alguns exemplos clicando na animação acima.
|
|
|
|
|
|
