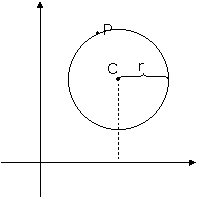
Descobrindo onde está um ponto P qualquer na circunferência
Um ponto P = (x,y) pode assumir três posições em relação a uma circunferência de raio r a centro C=(xc,yc) Para saber em qual destas situações um determinado ponto P = (x,y) se encaixa basta utilizar a equação geral da circunferência, como podemos ver no exemplo ao abaixo:
Imagine a circunferência
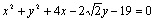 . .
Em que posição em relação a ela encontra-se o ponto P = (4, 4)?
Para resolver vamos substituir (4, 4) no primeiro membro da equação da circunferência dada, obtendo assim:
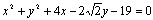
Portanto, o primeiro membro desta equação é igual a 17,72 (usando Ö2 =1,41). Este valor é maior que 0 e, por isto, podemos concluir que o ponto dado é externo a circunferência. Se este valor fosse menor que zero o ponto seria interno a circunferência, e se fosse igual a zero o ponto pertenceria à circunferência. |
 |
|
|
|
| |
O ponto P pode ser externo à circunferência
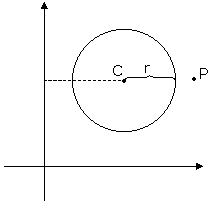 O ponto P pode ser interno à circunferência O ponto P pode ser interno à circunferência
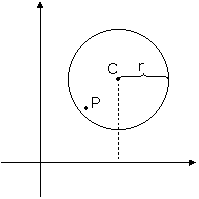 O ponto P pode pertencer à circunferência O ponto P pode pertencer à circunferência
 |
|
|
|
|
|