Inequações do primeiro grau
Uma das conseqüências do estudo de sinais de uma função é a possibilidade de resolver inequações.
Para relembrar, dada uma função f(x), chama-se inequação toda equação que pode assumir uma das seguintes formas:
f(x) > 0;
f(x) 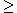 0; 0;
f(x) < 0;
f(x) 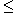 0 0 |
 |
|
|
|
| |
Então, resolver uma inequação do primeiro grau é encontrar os valores de x, para os quais f(x) assume uma das formas acima. Isto, foi exatamente o que fizemos quando estudamos os sinais de uma função do primeiro grau.
Para saber mais e ver alguns exemplos sobre inequações, clique aqui |
|
|
|
|
|