 |
|
|
| |
 |
Vamos fazer um gráfico de uma Função Afim
|
 |
|
|
|
|
|
| |
|
O gráfico de uma Função Afim f(x) = ax + b é uma ferramenta muito importante para que possamos fazer o estudo completo das propriedades desta função. Este gráfico será sempre uma reta, e sua posição no plano cartesiano ortogonal dependerá dos valores de a e b. Por causa disto, o estudo de uma Função Afim estará diretamente ligado com o estudo das retas na geometria.
|
|
|
|
|
|
| |
Bom, para entender mesmo é melhor acompanhar a construção do gráfico com exemplos. Clique em "Exemplos", no quadro ao lado e depois escolha uma função. Para a construção do gráfico montamos uma tabela com alguns valores para a variável x. Na verdade, por se tratar de uma reta precisamos de apenas dois valores de x para construir o gráfico (isto é visto em Geometria), mas nós vamos colocar mais alguns.
Em seguida, marcamos os pontos no plano cartesiano e os unimos obtendo a reta que representa a função.
|
|
|
|
|
|
|
|
| |
Observação:
A reta corta o eixo x quando f(x) = 0.
A reta corta o eixo y no ponto definido por f(0). E, de uma maneira geral, para uma função
f(x) = ax + b, com a#0
f(x) = 0 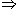 x = Neste caso x é chamado raiz da função.f(0) = bLogo, o coeficiente b será sempre a ordenada em que a reta intersecta o eixo y.
|
|
|
|
|
|
| |
Como determinar uma função afim conhecendo-se seus valores em apenas dois pontos?
Vimos que o gráfico de uma função afim, f(x) = ax + b, é uma reta. E pela geometria[link: geometria] para se traçar uma reta necessitamos apenas de dois pontos.
Com dois pontos distintos x1 e x2 tais que, f(x1) = y1 e f(x2) = y2 sejam conhecidos, podemos encontrar os valores de a e b da função f(x) = ax + b.Da seguinte forma:
para x1 # x2
|
|
|
|
|
|
|
|
