 |
|
 |
| |
 |
Área de um triângulo
|
 |
|
|
 |
|
 |
| |
Nós podemos calcular a área de um triângulo localizado em plano cartesiano. Para isto existe um requisitos:devemos conhecer as coordenadas de seus vértices.
Mas lembre-se! Para formar este triângulo precisamos de três pontos não alinhados no plano, ou melhor, deve existir entre eles uma determinante diferente de zero Se você quiser saber o porquê desta relação, clique aqui para voltar ao item de alinhamento entre três pontos.
|
|
|
 |
|
 |
| |
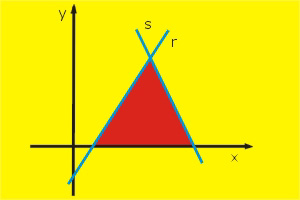
Veja este triângulo inserido no plano cartesiano e observe como (s) forma um dos lados do triângulos:
Matematicamente, temos a definição desta área como: Área do triângulo= ½.|D|. O que é D?
D representa o determinante entre as coordenadas dos pontos que podem formar o vértice do triângulo e que chamaremos de A,B e C. Definindo as coordenadas dos vértices A,B e C:
A tem como coordenadas (Xa,Ya)
B tem como coordenadas (Xb,Yb)
C tem como coordenadas (Xc,Yc)
|
 |
|
|
|
| |
|
|
| |
 |
|
| |
triângulo
|
|
|
|
|
|
|
|
 |
|
 |
| |
Pela fórmula da área teremos: 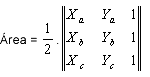
(sempre vamos considerar o resultado do determinante desta matriz na forma de seu módulo, isto é, se o resultado de D for –1, como módulo teremos 1)
|
|
|
 |
|
 |
| |
|
|
 |
|
 |