 |
|
 |
| |
 |
Posições relativas de duas retas
|
 |
|
|
 |
|
 |
| |
|
Aqui nós vamos conhecer as relações entre os coeficientes angulares de duas retas através das posições que ambas assumem em um plano cartesiano.
|
|
|
 |
|
 |
| |
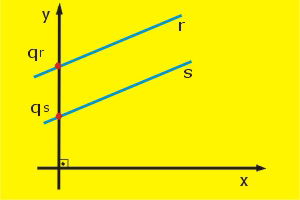
O que acontece se as retas são paralelas? Veja o gráfico:
Neste caso, sabemos que r//s, assim temos mr = ms
|
 |
|
|
|
| |
|
|
| |
 |
|
| |
Paralelo
|
|
|
|
|
|
|
|
 |
|
 |
| |
| Quando duas retas são coincidentes, temos r = s Û mr = ms e nr = ns. |
 |
|
|
|
| |
Vamos verificar se as duas retas abaixo são paralelas ou coincidentes. (r) 2x – y + 20 = 0
(s) 4x –2y + 1 = 0.
Determinando os coeficientes angulares de r e s nós vamos ter:
mr = 2 e ms=2, então mr = ms
Determinando os coeficientes lineares:
nr = -20 e ns = 1/2. Por estes valores podemos afirmar que r//s. |
|
|
|
|
|
|
|
 |
|
 |
| |
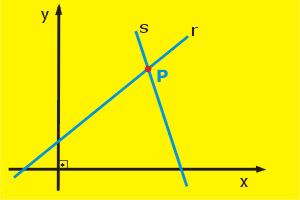
Retas concorrentes e perpendiculares Sabemos que duas retas são concorrentes quando ambas se cruzam. Observe a figura: Quando duas retas são concorrentes, temos:
r x s <==> mr ¹ ms Sendo que os coeficientes angulares ficam determinados por: ms = -1/ mr ou mr . ms = -1. Esta relação vale para as retas perpendiculares entre si, ou seja, quando uma delas produz sobre a outra um ângulo de 90°.
|
 |
|
|
|
| |
|
|
| |
 |
|
| |
Concorrentes
|
|
|
|
|
|
|
|
 |
|
 |