 |
|
 |
| |
 |
Gráfico de uma função
|
 |
|
|
 |
|
 |
| |
O gráfico da função f(x) = ax2 + bx + c, é uma curva chamada parábola, que você pode ver na figura ao lado.
O ponto V é denominado vértice da parábola. A parábola apresenta uma simetria em relação à reta que passa pelo vértice perpendicular ao eixo x.
Nosso trabalho agora é: a partir de uma função do segundo grau f(x), construir o seu gráfico. Lembre-se que o gráfico da função f(x) = ax2 + bx + c, depende dos coeficientes a, b e c de f(x).
Mas, antes de mostrar alguns exemplos numéricos, vamos descrever como fazer um esboço do gráfico da função de segundo grau. Os itens mais importantes estão detalhados abaixo.
(você pode acompanhar visualmente clicando na figura ao lado)
|
|
|
 |
|
 |
| |
1. Estudo da concavidade da parábola:
A parábola que representa a função f(x) pode ter concavidade voltada para baixo ou para cima:
Se a > 0, a concavidade da parábola será voltada para cima.
Se a < 0, a concavidade da parábola será voltada para baixo.
2. Zeros da parábola e intersecção com o eixo x:
Os pontos em que a parábola corta o eixo x são os zeros (ou raízes) da função f(x), e como se vê em zeros da função 2º grau, as raízes da função dependem do sinal do discriminante 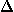 =b2-4a.c. =b2-4a.c.
Se 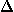 > 0 a parábola corta o eixo x em dois pontos, dados por: > 0 a parábola corta o eixo x em dois pontos, dados por:
Se 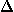 = 0 , a parábola toca (mas não corta!) o eixo x em apenas um ponto, dado por: = 0 , a parábola toca (mas não corta!) o eixo x em apenas um ponto, dado por:
Se 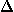 < 0 a parábola não corta o eixo x . < 0 a parábola não corta o eixo x .
|
 |
|
|
|
 |
|
 |
| |
3. Vértice da parábola:
O vértice da parábola é dado pelo ponto:
Além da ajuda na elaboração do gráfico, a determinação do vértice da parábola, permite determinar a imagem da função f(x), bem como seu valor máximo ou mínimo.
4. Intersecção da parábola com o eixo y:
A parábola sempre intercepta o eixo y em apenas um ponto. Este ponto é encontrado calculando o valor de f(x) no ponto x = 0. Mas f(0) = c, para toda função f(x) = ax2 + bx + c, assim podemos dizer que a parábola corta o eixo y no ponto:
(0, c) Continuar ->
|
|
|
 |
|
 |