 |
|
 |
| |
 |
Zeros (ou raízes) de uma função
|
 |
|
|
 |
|
 |
| |
Vamos aprender a reconhecer os zeros (ou raízes) de uma Função do Segundo Grau
Os zeros ,ou raízes, da função de 2º grau f(x) = ax2 + bx + c, são os valores de x, reais, quando :
f(x) = 0
|
|
|
 |
|
 |
| |
| Portanto, são todas as soluções da equação do segundo grau ax2 + bx + c = 0. A solução desta equação é feita através da fórmula de Bhaskara, que nos dá como raízes da função de segundo grau, os seguintes valores: |
 |
|
|
|
| |
onde D=b2-4.a.c é chamado discriminante da função f(x). |
|
|
|
|
|
|
|
 |
|
 |
| |
|
Observe que a existência de raízes reais, fica condicionada ao fato de ser um número real. Assim, temos três possibilidades:
|
|
|
 |
|
 |
| |
1) 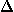 > b2-4.a.c > 0, então é um número real e a equação apresentará duas raízes distintas, dadas por > b2-4.a.c > 0, então é um número real e a equação apresentará duas raízes distintas, dadas por |
 |
|
|
|
 |
|
 |
| |
2) 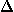 = b2 -4a.c = 0, então é um número real mas a equação apresentará duas raízes iguais, que são: = b2 -4a.c = 0, então é um número real mas a equação apresentará duas raízes iguais, que são:
3)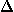 < b2 -4a.c = 0, então não é um número real e a equação não apresentará raízes reais. < b2 -4a.c = 0, então não é um número real e a equação não apresentará raízes reais.
|
|
|
 |
|
 |
| |
|
Para ver alguns “exemplos”, clique ao lado:
|
 |
|
|
|
 |
|
 |
| |
Soma e Produto de raízes
Veja a função f(x) = ax2 + bx + c, com a ≠ 0. Se tivermos 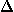 =b2 -4.a.c =b2 -4.a.c 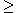 0 , f(x) terá duas raízes reais (não necessariamente distintas) que identificamos por: 0 , f(x) terá duas raízes reais (não necessariamente distintas) que identificamos por:
x1 e x2. Então a soma destas raízes será dada por:
.
e o produto será:
A partir destas relações podemos calcular as raízes de uma função do segundo grau. Isto quer dizer que para uma função f(x) = ax2 + bx + c, com   0, as raízes desta função serão dois números reais x1 e x2 tais que: 0, as raízes desta função serão dois números reais x1 e x2 tais que:
obs: encontrar estes números não é muito simples, principalmente se não forem números inteiros |
 |
|
|
|
| |
Fatoração da função de segundo grau
Na função do segundo grau f(x) = ax2 + bx + c,
se tivermos
D ³ 0
a função terá duas raízes reais x1 e x2.
E você ainda pode fatorar a função da seguinte forma:
f(x) = a.(x - x1).(x - x2) |
|
|
|
|
|
|
|
 |
|
 |