 |
|
 |
| |
 |
Equação geral da reta
|
 |
|
|
 |
|
 |
| |
|
Já vimos que três pontos estão localizados sobre a mesma reta se o determinante entre suas coordenadas for nulo. Podemos determinar a equação geral desta reta utilizando o conceito de alinhamento entre os pontos.
|
|
|
 |
|
 |
| |
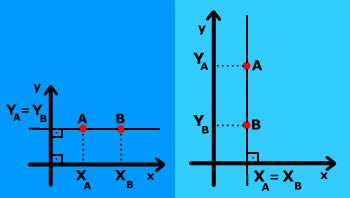
Observe o gráfico que representa o plano cartesiano:
Você pode observar que os pontos A, B e P estão na mesma reta r, desta maneira, podemos afirmar que o determinante entre as coordenadas dos três pontos é igual a zero. Vamos determinar que o ponto P tem como coordenadas (x,y) e os demais pontos, A e B tenham, respectivamente, as coordenadas (XA,YA) e (XB,YB). 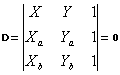
|
 |
|
|
|
| |
|
|
| |
 |
|
| |
Reta
|
|
|
|
|
|
|
|
 |
|
 |
| |
Quando resolvemos este determinante, encontramos a equação: (Ya-Yb)x + (Xa-Xb)y + (XaYb – XbYa) = 0
a.x + b.y + c = 0. Veja que chamamos de a todo o parêntese que multiplica o coeficiente X e, b de modo análogo, b todo o parêntese que multiplica o coeficiente Y e o termo independente.
|
|
|
 |
|
 |
| |
|
Como será a nossa equação geral da reta? a.x + b.y + c = 0, onde temos que a e b devem ser diferentes de zero.
|
 |
|
|
|
 |
|
 |